목차
A/B test에 대해 여러 자료를 찾아보다가
기초 통계지식부터 간단한 실습까지 설명해둔 문서가 없어서
그냥 내가 만들기로 했다.
A/B test는 Z-test(통계적 가설 검정)개념이 들어가 있는 만큼
통계학적 지식을 활용해 의사결정을 하는데 유용한 프레임워크이다.
그럼 차근차근 A/B test의 조각을 완성해나가보자
1. 기초 통계지식 [나부랭이 님 블로그 참고]
1-1) 통계적 가설 검정
우리는 많은 이론을 향유하며 살아간다.
그러나 그 이론은 새로운 가설에 의해 이의를 제기받게 되고
검증을 통해 새로운 가설이 패러다임을 대체하거나, 혹은 기존 이론은 그 자리를 굳건히 지키게 된다.

예를 들어 예전에는 태양이 지구 주위를 돈다는 천동설이 있었고
그 이후에는 지구가 태양을 돈다는 지동설이 가설로 제기되었다.
현재의 가설 vs 새로운 가설
이 두 가설 중 어떤 가설이 더 정확하고 신뢰성 있는지를 판단하는 것을 가설검정이라고 칭한다.
1-2) 귀무가설 vs 대립가설
이 중 현재 우리가 암묵적으로 믿는 가설을 귀무가설(H0)이라 하며
새롭게 제기된 가설은 대립가설(H1)이라 불린다.
즉 앞선 예시에서 두 가설을 비교해보자면 이렇다.
귀무가설 : 천동설(태양이 지구 주위를 돔)
대립가설 : 지동설(지구가 태양주위를 돔)
이 두 가설은 정반대로 설정되어야 하며 겹치는 중복부분이 없어야 한다
1-3) 검정 통계량
이렇게 가설이 설정되었다면 우리는 모집단의 특성을 추론하기 위해
여러 표본을 뽑아 표본 통계량을 계산하게 된다.
이 표본통계량을 가설검정에서는 검정에 사용하는 통계량이기 때문에
검정 통계량이라고 부른다.
검정 통계량은 그래프의 x축의 좌표로 표현된다.
예를 들어 정규분포라 한다면 우리가 표본통계량을 구했던 식을 통해
다음과 같이 검정통계량이 나온다고 할 수 있다.
 |
 |
| 정규분포 검정 통계량 식 | 검정통계량 모습 |
출처 : https://math100.tistory.com/75
1-4) 기각역
가설 검정은 대립가설과 귀무가설 중 하나를 선택하는 과정이다.
우리가 원래 믿던 이론 (귀무가설)을 채택하면 => 대립가설을 기각되게 되고
반대로 새롭게 제기된 이론(대립가설)을 채택하면 => 귀무가설을 기각하게 된다.
그러나, 그 과정에서 귀무가설이 옳음에도 귀무가설을 탈락시키는 확률이 생기는데
이 확률을 우리는 유의수준(알파)로 부른다.
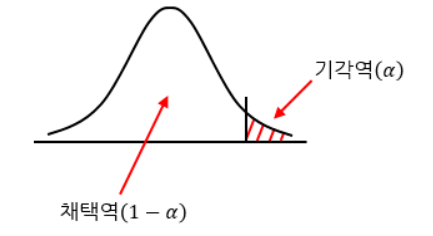
이 유의수준을 바탕으로
우리는 귀무가설을 채택하는 채택역과
귀무가설을 기각시키는 기각역을 설정할 수 있게 된다.

즉, 정리해보자면
검정통계량이 채택역에 속하게 되면 => 귀무가설 채택
검정통계량이 기각역에 속하게 되면 => 대립가설 채택
1-5) p-value
p-value란 귀무가설이 맞다는 전제하에 통계값이 실제로 관측된 값 혹은 그 이사으이 값이 나올 확률을 뜻한다.
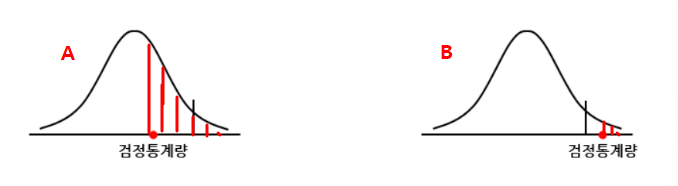
다음 A와 B그래프의 p-value를 영역으로 나타내면 다음과 같다.
즉, 우리는 표본 통계량인 검정통계량을 통해 p-value를 계산할 수 있다.
그리고 물을 수 있다.
표본으로 통계량을 내보았더니 평균적으로는 이 정도 통계량이 나오고
이 값이 나오거나 이 이상의 값이 나올 확률(p-value)는 이정도야.
그럼 이게 정상이야?
만약 그 확률이 기각역을 결정하는 유의수준(알파)- 0.05 or 0.01% 안에 있다면
우리는 이 상황이 비정상적이라 생각한다.
따라서 전제했던 귀무가설이 옳다는 전제를 기각시킨다.
반대로 유의수준보다 p-value가 높다면
우리는 이 상황이 일어날 수 있는 상황이라 생각한다.
따라서 전제했던 귀무가설이 옳다는 전제를 채택한다.
2. z-test란
Z-test는 말이 어렵지 정규분포를 활용한 통계적 가설검정이다.
예를 들면
[문제] 파이썬 코딩:평균 80점/ 표준편차는 15점
프로젝트를 활용한 파이썬 수업을 100명의 수강생의 실시
새로운 강의를 적용해본 결과
수강생 평균점수 => 85점--'
새로운 강의방식이 유의한 차이를 만들어내었는지 유의수준 0.05에서 검증해보자
이런 문제가 있다고 했을 때 가설 2가지를 세워보자.
귀무가설 : 새로운 강의 방식에 의한 변화는 없을 것이다. => u =80 (평균이 그대로 80)
대립가설 : 새로운 강의 방식에 의한 차이가 있을 것이다. => u≠80 (평균이 같지 않음)
유의수준 0.05라면 기각값은 1.96이다.
검정통계량은 다음과 같다.
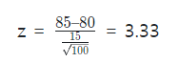
그럼 이게 기각되는지 채택되는지 살펴보자면

z-점수는 3.33이기 때문에 기각역이 1.96보다 커서 귀무가설을 기각한다고 할 수 있다.
# 효과크기
우리는 유의검정을 하며 p-value를 사용한다.
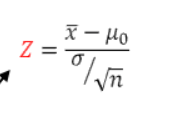
그러나 p-value를 결정짓는 것은 검정통계량이고
검정통계량은 표본크기에 민감하게 반응한다.
무엇보다 p-value는 그 정보가 통계적 유의성에 한정된다는 단점이 있다.
예를 들어
- 도쿄-런던 사람들의 평큔 키 차이 검정 : p-value : 0.01
- 베를린-파리 사람들의 평큔 키 차이 검정 : p-value : 0.001
그럼 베를린-파리 사람들의 키 차이에 대한 p-value가 더 작으니까
이 두 도시 사람들의 키 차이가 도쿄-런던 도시 사람들의 키 차이보다 더 크다고 결론내릴 수 있을까?
p-value의 역할은 두 도시의 키 차이가 통계적으로 유의하다는 것이지
p-value가 더 작다고 해서 그것이 더 큰 차이가 있는 것은 아니다.
즉 p-value가 작다고 해서
그것이 귀무가설이 얼마나 잘못되었는지를 의미하는 건 아니다.
그럼 이런 차이를 나타내는 통계량이 있을까?
그게 효과크기다.
Effect Size
: 변수들 사이의 관계가 얼마나 의미있는지
: 그룹들 사이의 차이가 얼마나 의미있는지
=> 따라서 effect-size가 크면 연구결과가 significance하며
=> 그것이 아니면 연구결과는 제한적임
즉, p-value는 통계적으로 유의한지를 나타내는 것이고
effe-tsize는 실제적 차이를 나타내는 지표이다.
예를 들어서
어떤 두 그룹의 차이가 3점이라는
대립가설에 대해 p-value가 0.002가 나오면
각각이 나타내는 정보는 다음과 같다.
p-value : 두 그룹 차이가 통계적으로 유의한가
effect_size : 3점이라는 차이가 얼마나 큰 차이인가
효과크기는 다음과 같은 지표로 측정가능하다고 한다.

3. A/B test [kaggle 사례 참고]
https://www.kaggle.com/code/richieone13/a-b-testing-example
a/b test란 집단을 두 그룹으로 나누고 상관관계와 인과관계를 측정하는 분석 프레임워크다.
즉, 두 집단의 차이가 통계적으로 유의한지 확인하는 z-test의 과정을 거친다고 볼 수 있다.
# 문제상황
그럼 간단한 실습을 통해 살펴보자
상황 : 어떤 테마가 웹 사이트 전환율이 더 높을까?
목적 : a/b test 를 통해 유입률에 영향을 주는 변인요소를 파악하고 비교해보자
note :funnel과 전환경로, 이탈률 추적을 고려하지 않은 간단한 실험임
#가설 설정
우리가 검증하고픈 것 : 새로운 디자인이 유입률에 더 좋은가? 아님 기존 디자인이 좋은가?
귀무가설(H0) : 새로운 디자인은 구리다. 기존유입률 이랑 별차이가 없다.
대립가설(H1) : 아니다! 새로운 디자인 좋다!
가정 : 유의수준은 5%
#변수 설명
대조군 vs 실험군
대조군 : 기존 디자인
실험군 : 새로운 디자인
=> 두 그룹의 유일한 차이를 디자인으로 설정
=> 두 테스트 결과의 차이를 디자인으로 귀인할 수 있도록 만듦
독립변수 - 종속변수
독립변수 : 디자인
종속변수 : 전환율
=> 디자인 변화에 따라 전환율이 어떻게 변하는가?
전환율 표기 이진코드화
0- 세션 안에 물건 안삼
1- 세션 안에 물건 삼
먼저 각종 pacakge와 효과크기 / 적정 표본량을 계산해놓자
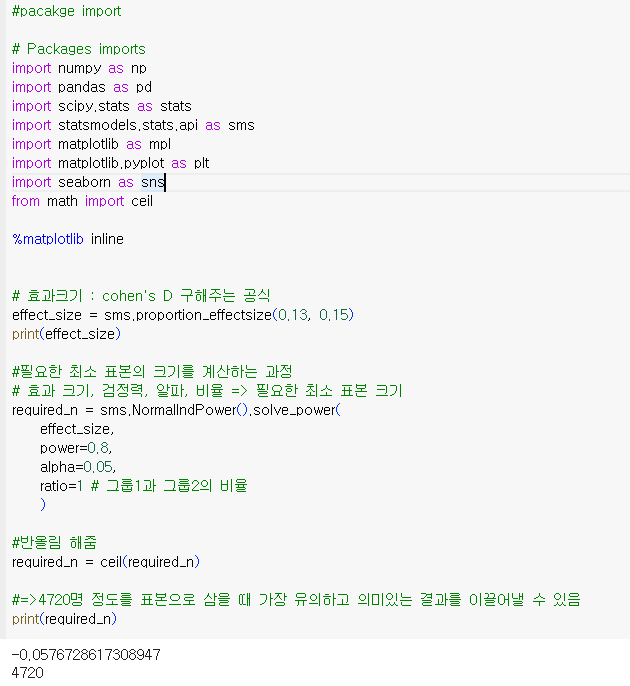
# 전처리 과정
데이터를 살펴봅시다.

실험/대조군별로 어떤 page에서 왔는지 살펴봅시다.

우리가 기대하는 데이터셋은
대조군 => old_page로부터 온 사람들
실험군 => new_page로부터 온 사람들
그런데 데이터가 섞여 있습니다.
아마 한 user가 여러번 방문한 적이 있는 것 같아요.
각 user 별로 방문횟수만 필터링해볼게요.

역시 재방문 기록들이 섞여있네요.
방문을 한번 이상 한 사람들은 분석하기가 애매해요.
우리는 페이지의 전환율 효과를 측정하고 싶은데
처음 이 페이지에 올때 어떤 걸 보고 왔는지 모르기 때문입니다.
방문 기록이 1번 이상인 사람들을 날려주겠습니다.

다시 한번 찍어보죠
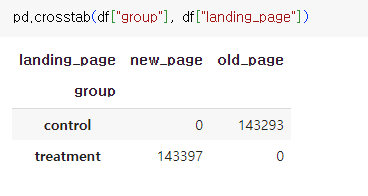
확실히 방문 기록이 하나 이상인 기록을 삭제하니 데이터셋이 깔끔해졌네요
대조군은 old_page로부터 유입된 사람만 남고
실험군에는 new_page로부터 유입된 사람들만 있어요
#Sampling : 표본 뽑기
pandas의 DataFrame.sample(표본 크기)를 사용할 겁니다.
근데 아까 가장 적당한 표본크기는 여러 파라미터를 통해 구해놨죠? (4720개)
그럼 각각 대조군과 실험군을 4720개씩 뽑아봅시다

이렇게 각각 control_sample(대조군)가 treatment_sample(실험군)이 나뉘어졌어요.
먼저 pd.concat()을 통해 한 테이블에 합쳐주겠습니다.

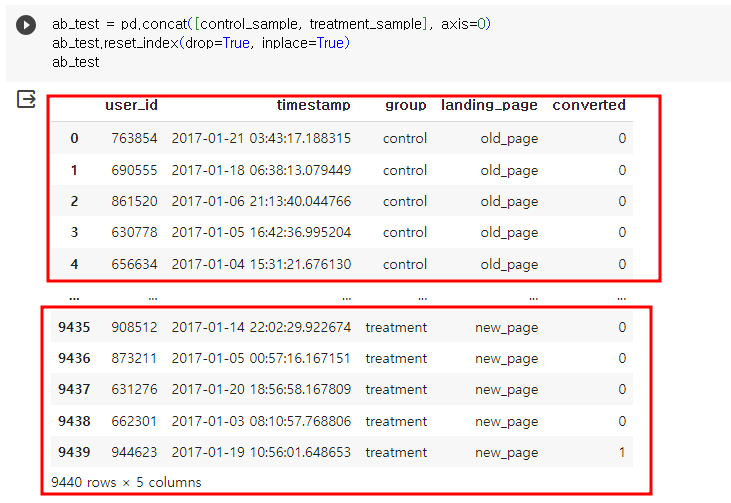

각각 4720개씩 잘 뽑힌 모습을 볼 수 있습니다.
# 결과 시각화
우린 z-test를 할거니까 표준정규분포를 그려야 되는데요.
따라서 각 실험군과 대조군 group별
- 전환율의 평균
- 표준편차
- 표준오차
이렇게 3가지가 필요해요 그래야 정규분포를 그릴 수 있으니까요
먼저 표준편차와 표준오차 구하는 함수를 정의해주고
# 표준편차와 표준오차 구하는 함수
std_p = lambda x: np.std(x, ddof=0)
se_p = lambda x: stats.sem(x, ddof=0)
각 그룹별로 그룹화를 해서 전환율만 집계해볼게요
#먼저 group별로 그룹화하고 converted만 집계해봅시다.
conversion_rates = ab_test.groupby('group')['converted']
그러니까 SQL코드로 하면 대충 이런 상황입니다.
select converted(전환되었는지)
from ab_test
group by group
이제 각 그룹의 평균, 표준편차, 표준오차를 구해봅니다.
conversion_rates = conversion_rates.agg([np.mean, std_p, se_p])
conversion_rates.columns = ['conversion_rate', 'std_deviation', 'std_error']
conversion_rates.style.format('{:.3f}')
conversion_rates.head()
결과를 한번 짚고 가보겠습니다.
우선 전환율 차이는 그리 커보이지 않아요
실험군의 평균 전환율이 0.003 정도 더 좋네요
이번 디자인은 망한 것 같다고 추론가능합니다.
그래도 디자인팀 보라고 한번 차이가 없는 막대그래프는 그려줘야죠
plt.figure(figsize=(8,6))
sns.barplot(x=ab_test['group'], y=ab_test['converted'], errorbar=('ci', False))
plt.ylim(0, 0.17)
plt.title('Conversion rate by group')
plt.xlabel('Group')
plt.ylabel('Converted (proportion)');
plt.show()

#Z-test 검증
이제 통계검증을 할건데요.
조금 어려워지는 부분이 있으니 집중해주세요!
먼저 z-test 라이브러리를 불러와줍니다.
from statsmodels.stats.proportion import proportions_ztest, proportion_confint
이제 실험군 과 대조군 데이터의 전환데이터를 구분해볼게요
#실험군의 전환데이터 / 대조군의 전환데이터 구분
control_results = ab_test[ab_test['group'] == 'control']['converted']
treatment_results = ab_test[ab_test['group'] == 'treatment']['converted']
각 그룹에서 전환 여부 데이터만 가져왔습니다.
각 데이터셋이 몇개인지 n_con과 n_treat에 저장해줍시다. (표본크기)
# 각 데이터셋이 몇개인지
n_con = control_results.count()
n_treat = treatment_results.count()
각 그룹에서 성공한 케이스들을 담아 리스트로 만들게요

실험군인 old_page의 전환성공 건수 : 582건
대조군인 new_page의 전환성공건수 : 593건
각 군의 데이터셋 길이도 리스트로 만들겠습니다.

그럼 z-test를 실행해보겠습니다.

음.. 이번 디자인은 심각하네요.
신뢰구간의 각 통계량값도 구해보겠습니다.

양측 검정을 할 때 기각역의 경계가 되는 통계량값들을 말합니다.
즉, 채택역의 구간을 말합니다.

그럼 지금까지의 통계값을 보겠습니다.

결론적으로 보면
p-value가 0.732인 만큼 0.05보다 너무 높습니다.
따라서 새로운 디자인은 완전 실패했네요
또한 treatement group의 신뢰구간에 목표였던 15%전환율이 포함되지 않습니다.
이는 새로운 디자인의 효과가 없으며 다시 디자인을 해야한다는 증거입니다.
4. 아티클 정리 [데이터리안]
출처 : https://datarian.io/blog/dont-be-overwhelmed-by-pvalue
A/B 테스트에서 p-value에 휘둘리지 않기
실험의 목적은 얼마나 효과가 있는지 살펴보는 것이지 통계적 유의성만을 확보하는 것이 아니다.
datarian.io
1) 효과크기를 무시한 유의성 검정
앞선 전환율의 차이는 0.3%이었죠 그럼 p-value 높다고 해서 이건 의미없는 정보일까요?
만약 하루 평균 1000명이 들어온다면 구매전환을 0.3%는 3명입니다.
그러나 1000만명이면 어떨까요?
3만명의 전환이 생깁니다. 중요한 것은 해당효과가 현실에서 어느정도 가치를 의미하는것인지 아는 것입니다.
따라서 단순 통계적 유의성(p-value)도 중요하지만
그것이 미치는 임팩트의 크기인 effect_size도 고려할 필요가 있습니다.
2. 적절한 표본크기 설정하기
실험시작 전에 적절한 표본을 설정하는 것이 중요합니다. 앞서 우리는 라이브러리를 사용해 계산을 했는데요. 아티클에서는 크게 2가지 요소가 필요하다고 이야기합니다.
- 유의수준 : 0,05
- 검정력 : 0.8

여기서 검정력이란 : 실제 효과가 있는데 있다고 판단할 가능성으로 1-B(2종오류)의 가능성으로 계산합니다.
검정력을 계산해주는 계산기도 따로 있고, 전반적으로는 0.8로 설정하는게 디폴트라고 하네요
3. 실험이 안끝났는데 결과 살펴보기
실험을 너무 오래끌면 표본이 쌓여서 표준편차가 낮아집니다.
그럼으로써 표본오차가 줄어들고 통계적 유의성을 띌 확률이 높아지죠.
반대로 실험이 안끝났는데 계속 엿보다가 유의성을 띌 때 실험을 중단하는 것도 문제라는 이야기입니다.
4. 아티클의 결론
결론부는 그대로 실어보겠습니다.
p-value는 통계적 실험에서 중요한 개념이 맞지만, 이것에만 휘둘려서는 안된다.
특히 A/B 테스트는 함께 고려할 요소가 많다.
유의 수준과 검정력, 탐지하고자 원하는 효과 크기를 정하고 이를 토대로 적정 실험 규모를 정해야 한다.
필요 이상으로 실험 규모를 키워서 과한(Overpowered) 실험을 하는 것은 자원 낭비고 잘못된 의사 결정을 이끌 수 있다. 반대로 실험을 자꾸 엿보다가 부족한(Underpowered) 실험을 하는 것은 오류에 빠질 가능성을 높인다.
현실적인 상황을 고려한 실험 운영도 필요한데, 전형적인 통계 실험 외의 대안을 찾아볼 필요도 있다.
실험 결과의 중요성을 한 번에 판단해 줄 마술 지팡이 같은 통계적 개념은 없다
.p-value는 통계적 유의성 확보를 위한 도구이지, 실험 결과의 중요성을 평가하는 지표가 아니다.
실험 결과가 현실적으로 어떤 중요성을 갖는지 판단해야 한다. 그 결과를 얼마나 믿을 수 있는지는 그 다음 문제다.
'데이터 분석' 카테고리의 다른 글
| 비전공생 SQLD 일주일 합격 후기 feat) 요약자료 및 준비방법 (0) | 2023.12.29 |
|---|---|
| [DB분석 실무 테크닉 100] ch2. 대리점 데이터를 가공하는 테크닉10 (0) | 2023.10.15 |
| [미니 프로젝트] Yammer case 분석2. 검색기능 문제 (0) | 2023.08.21 |


